価格はランダムに見える。しかし価格変動の大きさ(ボラティリティ)はランダムではない。静かな日が続くと静かさが続き、荒れると荒れやすい——ボラティリティのクラスタリング。ロバート・F・イングル三世(Robert F. Engle III, 1942–)は、この経験則を統計モデルに昇華し、ARCH(自己回帰的条件付異分散)を提案。のちに GARCH、非対称 GARCH、多変量GARCH、DCC(動学的条件付相関)へと発展し、金融リスク管理・政策評価・資産配分を一変させた。
2003 年、イングルはクライヴ・W・J・グレンジャー(コインテグレーション)とともにノーベル経済学賞を受賞。この記事では、経歴、主要理論、受賞理由と時代背景、世界・日本への影響、批判と限界、そして今日的意義(AI・高頻度データ・気候ファイナンス)までを、図解と実務チェックリスト付きで立体的に解説する。
1. 受賞者の経歴整理(出生地・学歴・主要ポスト)
出生:1942 年、米国ニューヨーク州シラキュース。
学 歴 : ウ ィ リ ア ム ズ ・ カ レ ッ ジ ( 数 学 ・ 物 理 ) 、 コ ー ネ ル 大 学 で Ph.D. ( 経 済 学 ,1969)。
主要ポスト:
UC サンディエゴ(UCSD)教授(1980 年代〜2000 年代初頭)——計量経済の名門を築く。
ニューヨーク大学スターン経営大学院(NYU Stern)教授、Volatility Lab(V-Lab)主宰。
主な受賞・活動:
2003 年ノーベル経済学賞(ボラティリティ分析の方法論)。
証券・規制当局、中央銀行、国際機関での助言。
小結:「分散は一定ではない」という一言を、実務の言語に変えた研究者。
2. 主要理論・研究内容
2-1. ARCH:誤差の大きさが自己回帰する

2-3. 非対称の取り込み:レバレッジ効果
EGARCH(Nelson):対数分散で負のショックの影響を強めに扱う。
GJR-GARCH(Glosten–Jagannathan–Runkle):負のリターンに追加項を入れて非対称に。
直観:悪いニュース→ レバレッジ上昇→ ボラ上昇が強い。
2-4. 多変量と相関:BEKK・DCC
BEKK(Engle–Kroner):分散共分散行列の正定性を保証。
DCC-GARCH(Engle, 2002):
各系列の分散はユニバリアント GARCH で推定。
相関係数を動学更新:マーケット間の連動性の変化を捉える。
図解(概念):
各資産の h_t(ボラ→ 標準化残差 相関→ Q_t を更新(DCC)
→時々の ” 連動 ”を推定(危機時↑)
2-5. リスク指標:VaR、ES、SRISK
VaR(Value-at-Risk):一定信頼水準での損失上限(分布仮定と尾の扱いに注意)。
Expected Shortfall(ES):VaR を超えた尾の平均損失(規制上の標準へ)。
SRISK(Acharya–Engle 等):金融機関の資本不足の期待値。システミック・リスクをボラと相関から測る指標。
2-6. 高頻度データと実現ボラ(Realized Volatility)
日中のリターンから実現分散を構築(Andersen・Bollerslev らの系譜)。
HAR-RV(Heterogeneous ARCH):日・週・月の階層でマルチスケールの記憶を表現。
GARCH×RV のハイブリッドで予測を強化。
3. 受賞理由と当時の経済状況(課題と答え)
3-1. 課題(1970–90 年代)
金融時系列は平均ゼロでも分散は動く。しかし古典的 ARMA は同分散を前提。
リスク管理・デリバティブ価格・政策評価に、分散の予測が不可欠だった。
3-2. イングルの答え
ARCH で条件付分散を時変にし、統計推定と予測を可能に。
GARCH, 非対称, 多変量, DCC へと拡張し、実務と政策に直結する枠組みを提供。
受賞の核:「ボラティリティをモデル化できる」ことを示し、金融リスクの可視化と制御への道を切り開いた。
4. 世界・日本への影響(政策・学問・日常)
4-1. 政策・規制
ストレステストや市場リスクの自己資本規制(VaR/ES)に GARCH 系が組み込まれる。
危機期には相関上昇(DCC)が確認され、資本バッファ・流動性規制の設計根拠に。
4-2. 金融機関・運用
リスクパリティ・ダイナミック・ヘッジで時変ボラを入力。
デリバティブ:インプライド・ボラと実現ボラのアービトラージやボラ・キャリー戦略。
4-3. 学問・実務
高頻度計量、ベイズ推定、状態空間モデルと融合。マクロでも不確実性ショックの測定に応用。
4-4. 日本の射程
為替・JGB・株式の DCC 監視でリスクオン/オフを把握。
個人投資:ボラティリティ・ターゲティングでドローダウン抑制。
5. 批判と限界
分布仮定:正規分布は裾が薄い。スチューデント t やスケールミックスでファットテールに対応。
ジャンプ・レジーム:危機の不連続は GARCH だけでは捉えにくい。ジャンプ拡張やMS-GARCH(マルコフ・スイッチング)を併用。
パラメータのドリフト:制度・市場構造の変化で定常性が怪しくなる。ローリング推定やスパース多変量で柔軟化。
相関の暴騰:危機時の**“全部一緒 問題” **。DCC の上限バイアスや同時性に注意。
内生性:VaR 制御が自己実現的ボラ拡大を招く恐れ(デレバレッジの同時化)。
位置づけ:GARCH は基礎言語。だがジャンプ・レジーム・極値・制度を併記するのがプロの流儀。
6. 今日的意義(AI・気候・サイバー・地政)
6-1. AI×GARCH
機械学習の非線形予測(LSTM, GBM)と GARCH の構造(分散方程式)をハイブリッド化。解釈性と安定性を両立。
6-2. 実現ボラとマクロ不確実性
ニュース指標・テキスト不確実性(新聞・議事録)と DCC で、政策ショックの波及を計測。
6-3. 気候ファイナンス
気象極値とコモディティ・保険市場のボラ連関。再保険と CAT ボンドの相関管理に DCCの素養を。
6-4. サイバー・地政
イベントジャンプを極値理論(EVT)で補完。早期警戒ダッシュボードでレジーム移行を検出。
7. 図解でつかむイングルのコア
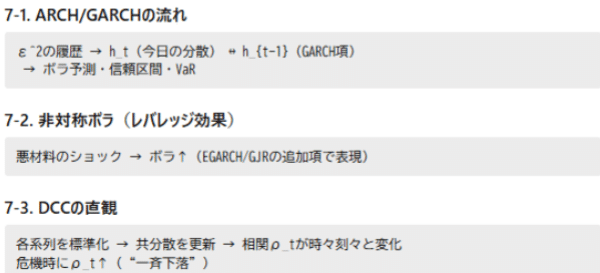
8. ケーススタディ(応用)
8-1. 運用:ボラターゲティング×リバランス
目標ボラ(年率 10%など)に合わせて資産配分のレバレッジを調整。GARCH 予測でシグナルを作り、取引コストとドローダウンのトレードオフを管理。
8-2. 規制・監督:ストレスと相関
ベースラインは GARCH、ストレスでは相関上振れ(DCC×EVT)を仮定。ES ベースの資本賦課を評価。
8-3. 企業財務:為替ヘッジ
円安局面のレバレッジ効果を織り込んだ動的ヘッジ比率。ボラ連関で輸出・原材料のヘッジを統合。
8-4. 個人:長期積立のメンタルモデル
ボラのクラスタリングを知れば、荒天時の過剰反応を抑えられる。定率リバランスで“荒天は過ぎる”に賭ける。
9. 研究の広がりと後継
長 期 記 憶 ( FIGARCH, HYGARCH ) 、 高 頻 度 の マ イ ク ロ 構 造 ノ イ ズ 、Realized-GARCH(Hansen–Huang–Shek)などが派生。
スパース多変量やネットワーク GARCH で次元の呪いに対応。
V-Lab は、株・債・為替・コモディティ・暗号資産までのボラと相関を日次で推定・公開。
10. FAQ(誤解の整理)
「GARCH(1,1)で十分?」→ベースには強い。ただし非対称・ジャンプ・レジームで頑健化を。
「VaR は危機で役立たない?」 → ES・EVT と併用し、モデルリスクを明示すれば有用。
「相関は一定?」→いいえ。 DCC で時変が標準認識。
「日次データで全部わかる?」→高頻度 RV でインプット強化を。
11. 実務者チェックリスト(運用・リスク・政策)
分布選択:t 分布・スケールミックスを用意(尾の厚さ)。
非対称テスト:レバレッジ効果の有無を検定(EGARCH/GJR)。
DCC 監視:危機時の相関上振れを想定。
EVT/ES:尾部の推定と ES 報告を標準化。
モデル合議:GARCH×RV×LSTM の委員会予測で頑健化。
ガバナンス:モデル検証(バリデーション)、再推定頻度、トリガーを文書化。
12. まとめ 「見えない変動」を可視化する力
イングルの計量経済学は、変動そのものを予測対象にした点で画期的だった。 ARCH/GARCH は、静かな日と荒れる日の記憶を数学にし、DCC は市場同士の連動のうねりを測る。AI や高頻度データ、気候リスクの時代に、波打つリスクを見える化し、意思決定に織り込む——その発想はこれからも中核であり続ける。
さくらフィナンシャルニュース
YouTube
https://www.youtube.com/@sakurafinancialnews



































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































-永井友理-190x190.jpg)
-永井友理-190x190.jpg)




参議院選挙立候補宣言-190x190.jpg)






























































































この記事へのコメントはありません。